本日のジャニ丸の勉強部屋では、
中1数学の正負の数の「正負の数の乗法・除法」を勉強するよ!
いよいよ、かけ算・わり算だね!
これまでの「加法・減法」よりも単純だからあんしんして!
加法・減法が不安だったら、早めに復習しておいてね。
早めの見直しが大事だよ!
>>「正負の数の加法・減法」を復習する

今日は、正負の数の乗法・除法、
かけ算・わり算をやっていくね!

乗法(じょうほう)、
除法(じょほう)・・・
読み方が似ててややこしいね。

乗法は「かけ算」
除法は「わり算」って覚えていいよ!

かけ算、わり算なら任せて!
小学校でもやったし!

正負の数の乗法・除法は、
符号のルールさえ覚えちゃえば大丈夫。
これからそのルールを説明するね。

うん!
お願いします!
同符号どうしの乗法・除法

まずは、同符号どうしの乗法から。
プラス × プラスとか、
マイナス × マイナスとか。

同符号どうしの乗法は、
符号はプラスになるって覚えて!

りょうかい!
同符号どうしのかけ算はプラスだね!

たとえば、下のような計算。
2つとも同符号どうしの乗法だよね。


うん!
+どうしと、-どうし。
同じ符号どうしのかけ算だね。

同符号どうしのかけ算は、
+ の符号をつけて数字を掛けるだけ。


おおお!
なんかカンタンかも!

実は、加法・減法よりも、
乗法・除法のほうがカンタンだよ!

除法(わり算)も同じ考え方でいいの?

そう!同符号どうしの除法も同じ。
プラス ÷ プラスとか、
マイナス ÷ マイナスのように、
同符号どうしの割り算も符号はプラスになるよ!


これ、できる!
(+8)÷(+2)= +4
(-9)÷(-3)= +3

バッチリだよ!


(+)×(+)=(+)
(-)×(-)=(+)
(+)÷(+)=(+)
(-)÷(-)=(+)
・・・って覚えてもいいよ!
- 同符号どうしの乗法・除法は、符号はプラスになる。
- (+)×(+)、(-)×(-)は、プラスになる。
- (+)÷(+)、(-)÷(-)は、プラスになる。
異符号どうしの乗法・除法

次は、異符号どうしの乗法・除法。
プラス×マイナスとか。
マイナス÷プラスとか。

異符号どうしの乗法・除法は、
符号はマイナスになるって覚えて!

さっきの「同符号どうし」と逆だね!
異符号どうしはマイナスになるんだね。

そう!
下の式は異符号どうしだよね。


これもできそう!
(-4)×(+2)= -8
(+8)÷(-2)= -4

すごーい!
異符号どうしも大丈夫だね!


(+)×(-)=(-)
(-)×(+)=(-)
(+)÷(-)=(-)
(-)÷(+)=(-)
・・・って覚えてもいいよ!
- 異符号どうしの乗法・除法は、符号はマイナスになる。
- (+)×(-)、(-)×(+)は、マイナスになる。
- (+)÷(-)、(-)÷(+)は、マイナスになる。
3数以上の乗法・除法

ここでは、
3数以上の乗法・除法をやるよ。
たとえば、
-5 × 2 ×(-3)とか。

OK!

ここでも大事なのは符号。
答えがプラスになるのか、マイナスになるのかがポイントになるよ。

さっきやったのは、
同符号どうしならプラス、
異符号どうしならマイナスだったよね。

そう。
でもそれは、2数の計算のとき。
たとえば、
(-)×(-)×(-)の場合は、
同符号どうしだけど符号はマイナスになるの。

え?そうなの?

じゃあ、下の式でやってみるね!
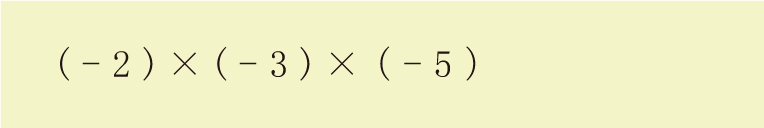

まずは、左から順番に計算するよ!


ほんとだ!
(-)×(-)で(+)になって、
(+)×(-)で(-)になった!

除法(わり算)も同じだよ。
下の計算、やってみて!
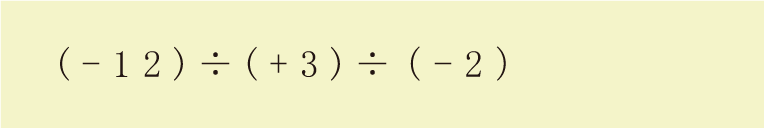

まかせて!

左から順に計算すると・・・
(-12)÷(+3)は、異符号だから、-4になる。
(-4)÷(-2)は、同符号だから、+2になる。


すごーい!
合ってるよ!!

やった!!
いえーい!!

これは、乗法と除法が混じった計算でも同じだよ。

ここからは不要なカッコを外すね。
下の計算、できる?


やってみる!
たぶんできる!!


どう!

ジャニ丸!かんぺき!
数字の前に符号がないときは、
プラスの符号が隠れているってことも覚えておいてね!

やったあ!
正負の数の乗法・除法は得意かも!

加法・減法よりカンタンでしょ!
気をつけるのは符号だけだからね。

ここでもうひとつ。
乗法・除法の計算では、符号の付け方にコツがあるの。

コツ…?

さっきやった計算を振り返るね。
①(-2)×(-3)×(-5)
②(-12)÷(+3)÷(-2)
③ 6×(-2)÷3

うん。答えは、
①は、-30
②は、+2
③は、-4 だった。

それぞれの式の、
マイナスの数に注目して!

①(-2)×(-3)×(-5)
この式にマイナスは何個ある?

①(-2)×(-3)×(-5)
マイナスは3個ある!

マイナスの数は3個で、
答えの符号はマイナスだったよね。

じゃあ次の式。
②(-12)÷(+3)÷(-2)
この式にマイナスは何個ある?

②(-12)÷(+3)÷(-2)
マイナスは2個だ!

マイナスの数は2個で、
答えの符号はプラスだったよね。

じゃあ最後の式。
③ 6×(-2)÷3
この式にマイナスは何個ある?

③ 6×(-2)÷3
マイナスは1個だね!

マイナスの数は1個で、
答えの符号はマイナスだったよね。

マイナスの個数で何がわかるの?

マイナスが1個だと答えはマイナス。
マイナスが2個だと答えはプラス。
マイナスが3個だと答えはマイナス。
ここでクイズ!
マイナスが4個だと答えの符号は?

プ、プラス・・・?

そう!
マイナスが5個だと?

マイナスだ!!

正負の数の乗法・除法だけの式は、
マイナスが奇数だと答えはマイナス。
マイナスが偶数だと答えはプラスになるの!

ホントだ!

ポイントはマイナスの個数だよ。
プラスは省略されることが多いから、マイナスの個数を数えてね!

ちなみに、マイナスが0個のとき。
これも答えはプラスになるからね!

オッケー!
マイナスの個数を数えるんだね!

じゃあ、下の計算を解いてみて!
わかりやすく絶対値は「1」にしたよ。
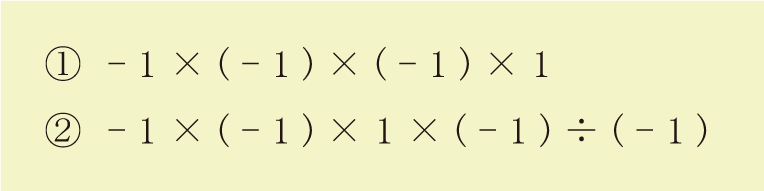

おおおお!
ぜんぶ「1」だ!
これなら、何回掛けても割っても「1」になるからラクだね!

ここでは、答えの符号がプラスかマイナスかを意識して解いてね!

マイナスの個数が偶数ならプラス、
マイナスの個数が奇数ならマイナスだから…


大正解!
マイナスの個数を数えるのは、ぜんぶ乗法・除法のときだけだからね!
- 3数以上の乗法・除法の計算では、マイナスの個数が奇数のときは答えはマイナスになる。
- 3数以上の乗法・除法の計算では、マイナスの個数が偶数のときは答えはプラスになる。
- プラスの符号は省略されることが多いので、マイナスの個数を数えた方がいい。
- マイナスが0個のときは、答えはプラスになる。
問題を解いてみよう!

問題だして~!

+ や( )を省いている式もあるよ。
マイナスの個数に気をつけてね!


みんなできた~?
この真下にある「答えを見る」をクリックすれば、答えが開くよ。
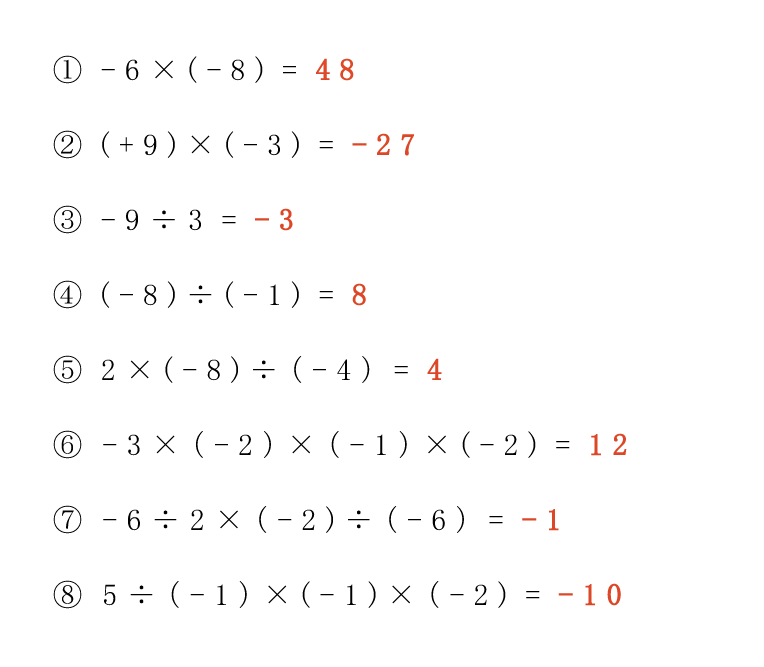
今回は、「正負の数の乗法・除法」を勉強したね。
かけ算・わり算のことだったけど、答えの符号がプラスになるかマイナスになるかが大事なポイント。
3数以上なら、マイナスの数を数えてね!
ここではまだまだ序ノ口。
正負の数の乗法・除法はまだまだ続くよ。
次の勉強部屋では「乗法の交換法則・結合法則」を勉強するよ。
かけ算どうしなら計算の順番を変えてもいいってやつ。
加法でもやったよね!
次回の勉強部屋はこちら!
>>乗法の交換法則・結合法則
