本日のジャニ丸の勉強部屋では、
中1数学の正負の数の「乗法の交換法則・結合法則」を勉強するよ!
前にも「加法の交換法則・結合法則」をやったけど、加法(たし算)だけじゃなくて、乗法(かけ算)でも同じことができるんだよ。
計算がラクになるから絶対にマスターしてね。
乗法・除法の基本や、加法の交換法則・結合法則が苦手な子は早めに復習をしておいてね。
早めの見直しが大事だよ!
>>「正負の数の乗法・除法」を復習する
>>「加法の交換法則・結合法則」を復習する

交換法則と結合法則、
前に「加法」でもやったね!

そうだね!
乗法にも「交換法則」と「結合法則」があるんだよ!

じゃあ、かけ算も順序を変えてもいいってこと?

その通り!
2×5も、
5×2も、同じ答えでしょ?

ホントだ!同じ「10」になる!

乗法の交換法則・結合法則もとっても便利だから、しっかり理解してね!

うん!
がんばるぞ!

まずは、
「乗法の交換法則」からやるね!
乗法の交換法則とは?

乗法の交換法則。
教科書にはこう書いてあるよね。
a × b = b × a

うん。加法と同じだ!
乗法(かけ算)も数を入れ替えてもいいってことだね。

そうだよ。
でも除法(わり算)は数を入れ替えちゃダメだからね。

たとえば、
4÷2の順序を変えて、
2÷4にしちゃうと答えが変わっちゃうよね。

4÷2=2
2÷4=0.5
答えはちがうね。

乗法は交換法則が使えるけど、
除法には使えないからね。

オッケー!
加法の交換法則のときも、
減法には使えなかったらから同じだね。

あと、乗法の交換法則も、
負の数が入っていても大丈夫。
-5×4=-20
4×(-5)=-20

ホントだ!
同じ答えだね。


負の符号がついた式では、
符号も一緒に入れ替えるってことも忘れないでね!
- 乗法の交換法則によって、かける数とかけられる数を入れ替えても答えは同じになる。
- 負の数が含まれていても、乗法の交換法則は成り立つ。
乗法の結合法則とは?

次は、乗法の結合法則。
教科所にはこう書いてある。
( a × b )× c = a ×( b × c )

乗法なら、
計算の順序を変えてもいいってことだね。

そう!
乗法の式はどこから計算してもいいの。
これも加法と同じだよ。

順序を変えて工夫することで、
計算が早くラクになるんだよね!

そう!順序を変えることで、
計算がとってもラクになることがあるの。

たとえば、
-12×4×(-25)

左から順番に計算すると、
すごくメンドクサイ…。


順番を変えて、
右から計算してみて!

OK!
やってみる!


どう?

すごくカンタンにできた!
ひっ算しなくて済んだ!

でしょ!3数以上の乗法では、
キリの良い数になるのがあれば、
先に計算すると楽だよ!

すごい!
かけて50や100、300みたいに、
下一桁が0になれば計算しやすいね!

他にもこんな計算。
-3×2×6×(-5)
どう計算する?

まかせて!
左から順にかけていくと、
-3×2×6×(-5)
=-6×6×(-5)
=-36×(-5)
ひっ算が必要になって面倒くさい!

順序を変えて、
最初の -3×2 と、
最後の 6×(-5)を先にやると…


ちょーカンタンにできた!

ジャニ丸!すごい!
乗法の結合法則も大丈夫だね!
- 乗法の結合法則によって、計算の順序を変えても答えは同じになる。
- 負の数が含まれていても、乗法の結合法則は成り立つ。
- 計算の順序を工夫することで、ひっ算が不要になるなどスムーズに計算できるようになるケースもある。
逆数で除法を乗法に変えよう!

乗法の交換法則・結合法則って、
計算しやすくなるから便利だね!

でしょ!
乗法の計算では役に立つよね!

除法も簡単になればいいのに…
(わり算、キライ…)

ジャニ丸、
「逆数」を使えば除法を乗法に変えられるよ!

ええ!!そうなの!?
「ぎゃくすう」ってなに?

今から「逆数」を説明するね。
そんなに難しくないから安心して!
逆数ってなに?

逆数・・・
教科書にはこう書いてあるね。
2つの数の積が1になるとき、一方の数を、他方の数の 逆数 といいます。
これは、負の数でも同じです。

う、う・・・
わけわかんない・・・

文章だと難しいよね。
でも数字でやるとカンタン!
まずは分数で考えていくよ。

おねがいしまっす!

分数を逆数にするときは、
分母と分子を入れ替えるだけ!
カンタンでしょ!


おお!カンタンだ!
分数は分母と分子を入れ替えれば逆数になるんだね!

分数の逆数は簡単。
整数や小数なら、分数に直してから逆数にするといいよ!

整数や小数を逆数にした例を見て!


なるほど!
整数や小数は、分数にしてから分母と分子を入れ替えると逆数になるんだね!

整数や小数はひと手間あるけど、
そんなに難しくなかったでしょ?

うん。カンタンだった。
負の数の場合はどうするの?
符号を変えたりするの?

すごくいい質問!
逆数にしたら、符号は変えちゃダメ!
かけたら 1 になるのが逆数だけど、
符号を変えると -1 になっちゃうからね!


りょうかい!
逆数は符号を変えないんだね!
- 逆数は、かけたら「1」になる数。
- 分数は分母と分子を入れ替えると逆数になる。
- 整数や小数を逆数にするときは、分数に変えてから分母と分子を入れ替えるとカンタン。
- 逆数にするときは、符号は変えてはいけない。
除法を乗法に変えよう!

逆数がわかったら、いよいよ実践!
除法を乗法に変えていくよ!

逆数にすれば、わり算をかけ算に変えられるんだよね!

たとえば下の式。
除法(わり算)が含まれているから、
交換法則や結合法則が使えない…。


うん。
除法があると順番変えられないからね。

じゃあ逆数を使って、
除法を乗法に変えるから見てて!


おお!全部かけ算になった!
これなら計算がすごくラクだね!

じゃあ、計算してみて!
できるだけ工夫して簡単にしてね!

まかせて!
「-2 と -5 を先に掛ければ…」


すごーい!!
だいせいかい!!

逆数、チョー便利だね!
全部かけ算にすると計算しやすい!

そうだね!
乗法だけの式にすれば、交換法則や結合法則が使えるから計算がラクになるよね!
問題を解いてみよう!

問題だして~!

除法が含まれている式は、
逆数にして乗法だけの式にしてね!
交換法則や結合法則を使って、工夫しながら計算してね!


⑤ が難しいよね…。
この真下にある「答えを見る」をクリックすれば、答えが開くよ。
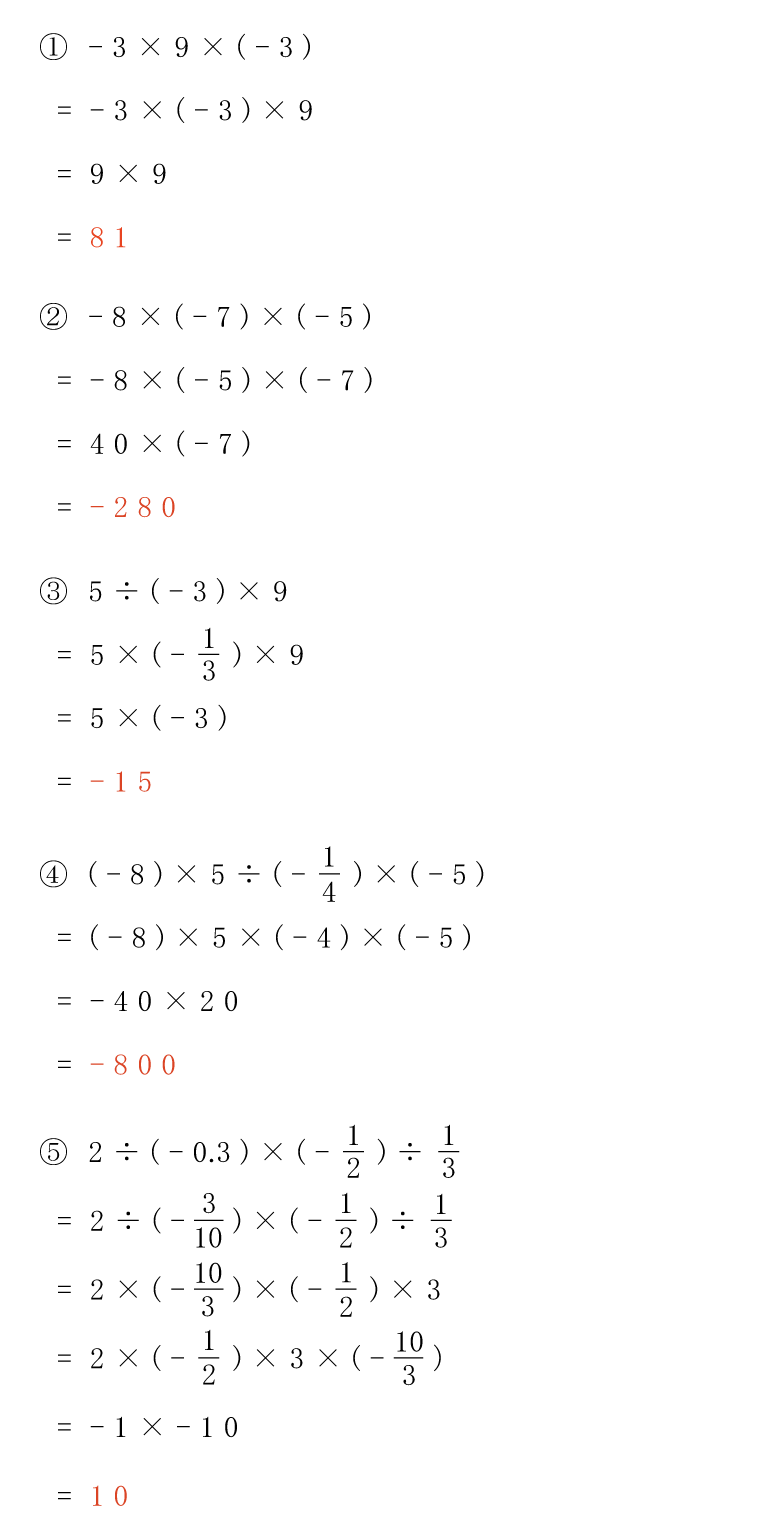
今回は、「乗法の交換法則・結合法則」を勉強したね。
乗法も加法と同じように、計算の順序を変えると計算がしやすくなるよ。
除法を乗法に変える「逆数」も大事な基本だからね!
正負の数の乗法・除法はもう少し続くよ。
次の勉強部屋では「指数をマスターしよう!」を勉強するよ。
2乗とか3乗ってやつだけど、負の数やカッコの有り無しで間違えやすいから気をつけて!
次回の勉強部屋はこちら!
>>指数をマスターしよう!
