本日のジャニ丸の勉強部屋では、
中1数学の正負の数の「素数と素因数分解」を勉強するよ!
これまで小5で習っていた「素数」と、中3で習っていた「素因数分解」が、2021年度から中1の正負の数で学習することになったんだよ。
素因数分解は、中3で習う「平方根」ってやつでも出てくるから、ここでしっかり理解しておいてね。
ここで出てくる数は自然数だけだから、負の数や分数・小数は出てこないよ。
早めの見直しが大事だよ!
>>「分配法則をマスターしよう」を復習する
>>「正負の数の乗法・除法」を復習する
>>「四則の混じった計算」を復習する

今日は「素数と素因数分解」だね。
”そすう”って聞いたことある!

「素数」は小5の算数でも習ったよね。
ここではもっと本格的にやるよ!

オッケー。
”そいんすうぶんかい”は難しい?

「素因数分解」は、素数の理解とかけ算・わり算ができれば難しくないよ!

よかった!
今日もよろしくね!
素数ってなに?

まずは「素数」から。
教科書にこう書いてあるね。


え?え?ええ??
約数ってなんだっけ?

約数は、ある数を割り切ることができる自然数のこと。
たとえば、
6 の約数は、1、2、3、6。
8 の約数は、1、2、4、8。

それ!やった!
思い出した!

素数っていうのは、
1 とその数しか約数がない自然数だよ!

じゃあ 6 は素数じゃないね。
約数が 1、2、3、6 だから!

その通り!
じゃあ 3 はどう?

3 の約数は、1 と 3 。
だから 3 は素数だ!

正解!
2、3、5、7、11、13 とかも、
1 とその数でしか割り切れないから素数だね。

あと、
1は素数に含めないから気をつけてね!

オッケー!
1 は素数に含めてはいけないんだね。

素数は他にもたくさんあるんだけど、
素数の倍数は素数じゃないってことを覚えておくと便利だよ。

例えば 3 は素数だけど、
3 の倍数、6、9、12、15 … は素数じゃないの。

うんうん。
じゃあ 7 の倍数( 14、21、28… )も素数じゃないんだね。

その通り。じゃあ問題ね。
55 は素数?

55 は 5 の倍数だ!
だから、素数じゃない!

じゃあ 17 は?

17 は…
2、3、5、7 で割り切れないから…
17 は素数だ!

すごーい!
大正解!

素数は無限にあるんだけど、
100 以下の素数は覚えておいてもいいかもね。

10 以下の素数は、2、3、5、7 の4個だね。
100 以下の素数って何個あるの?

100 以下の素数は 25個だよ。
エラトステネスのふるいで見てみるね!


この方法は、紀元前200年前に古代ギリシャの数学者エラトステネスが発見したと言われてて、「エラトステネスのふるい」って呼ばれてるんだって。

ふーん。
頭のいい人っているんだね…

100以下の素数を全部覚えるのは大変だけど、2,3,5,7,11,13,17,19,23,29 くらいまでは暗記しておくのがオススメだよ!
- 1とその数のほかに約数がない自然数を「素数」という。
- 1は素数に含めない。
- 素数の倍数は素数じゃない。
- 30 以下の素数は暗記しよう!
素因数分解とは?

素数がわかったところで、
いよいよ「素因数分解」だよ!

OK!
ゆっくり教えてね。

教科書にはこう書いてあるね。


「素数だけの積」ってことは、
素数どうしのかけ算にするんだね。

その通り!じゃあ、
6 を素因数分解するとどうなる?

6 を素因数分解すると…
2 × 3 になる!

正解!2 も 3 も素数だからね。

じゃあ次。
42 を素因数分解してみて。

え、えっと…
6 × 7 …??

ざーんねーん!
たしかに、6 × 7 は 42 になるけど、
6 は素数じゃないよね。

たしかに…。
素因数分解は、素数だけの積だからね…

じゃあもう一回。
42 を素因数分解して。

42 は、6 × 7 になる。
6 は、2 × 3 になるから、
42 = 2 × 3 × 7 だ!

正解!
素数だけの積にするのを忘れないでね。

あと、
2 × 2 とか、3 × 3 × 3 みたいに、
同じ素数どうしの積があったら、
指数を使って表してね。
- 自然数を素数だけの積にすることを、素因数分解という。
- 同じ素数の積は、指数を使って表す。
素因数分解の手順を覚えよう!

さっきやった 42 の素因数分解だけど、
2 × 3 × 7 ってどうやって出した?

42 は、6 × 7 で…
さらに 6 は、2 × 3 だから…
2 × 3 × 7 になった。

頭の中でやった!
もしかして天才かも!!

じゃあ、天才のジャニ丸くんに問題。
378 を素因数分解してみて。

378 ?
そんなのムリ…

378 のように大きい数になると、
頭の中だけでは難しくなるよね。

どうやってやるの~?

これから手順を説明するから、
ノートに書きながら練習してね!





おおおお!
素因数分解できた!

小さい素数から分解するんだよ。
偶数なら 2 で割り切れるし、
奇数なら 3 で考えてみて!

2、3 で割り切れなかったら 5 。
5 でも割れなかったら、
7 で割ってみるんだね!

7 でも割り切れなかったら 11 。
11 でも割り切れなかったら 13 だよ!

つまり、素数はある程度は覚えておくことが大事ってこと!
- わり算のひっ算を逆さまにした形で素数で割っていく。
- 小さい素数から順に割っていく。
- 素数はある程度まで覚えておく。
割り切れる素数を見つけるコツ

偶数なら 2 で割れるのはわかるけど、
他に割り切れる素数を見つけられるコツとかないの?

割り切れる数を見つけるコツはあるよ!
とっても便利だから覚えておいてね!

コツがあるんだ!
おしえて~!

ここでは、
2,3,5 で割り切れる形を見ていくね。

まず「2」で割り切れる形。
これは、下一桁が偶数だったよね。
14 とか 32 とか 128 とか。

うん!これはわかる!
偶数なら 2 で割り切れるからね!

次に「3」で割り切れる形。
ちょっと難しいけど、
全ての桁の数を足して 3 の倍数になるかで判断するの。

よくわかんない…

たとえば「177」。
全部の桁数を足すと、1+7+7=15
15 は 3 で割り切れるから、
「177」は 3 の倍数ってこと。

桁の数を全部足して、
3 の倍数かを調べるんだね。

じゃあ問題ね。
「2151」 は、3 の倍数?

まかせて!「2151」 だから…
2+1+5+1=9
9 は 3 で割り切れるから、
「2151」 は、3 の倍数だ!

OK!もう1問。
「253」は、3 の倍数?

「253」だから…
2+5+3=10
10 は 3 で割り切れないから、
「253」は、3 の倍数じゃない!

せいかい!
3 の倍数かを調べる方法はとっても便利だから、絶対に覚えておいてね!

次は「5」で割り切れる形。
下一桁が、0 か 5 なら 5 の倍数だよ!

5 の倍数は簡単だね。
下一桁が、0 か 5 だから、
215 とか 670 とかだよね!

そう! 5 の倍数も簡単だね。
- 2で割り切れる…下一桁が偶数
( 12、26、208 など ) - 3で割り切れる…すべての桁の数を足して3の倍数
( 153、321、1257 など ) - 5で割り切れる…下一桁が0か5
( 140、235、5625 など )
問題を解いてみよう!

問題だして~!

素因数分解は「習うより慣れろ」だよ。
たくさん問題を解いてね!


この真下にある「答えを見る」をクリックすれば、答えが開くよ。
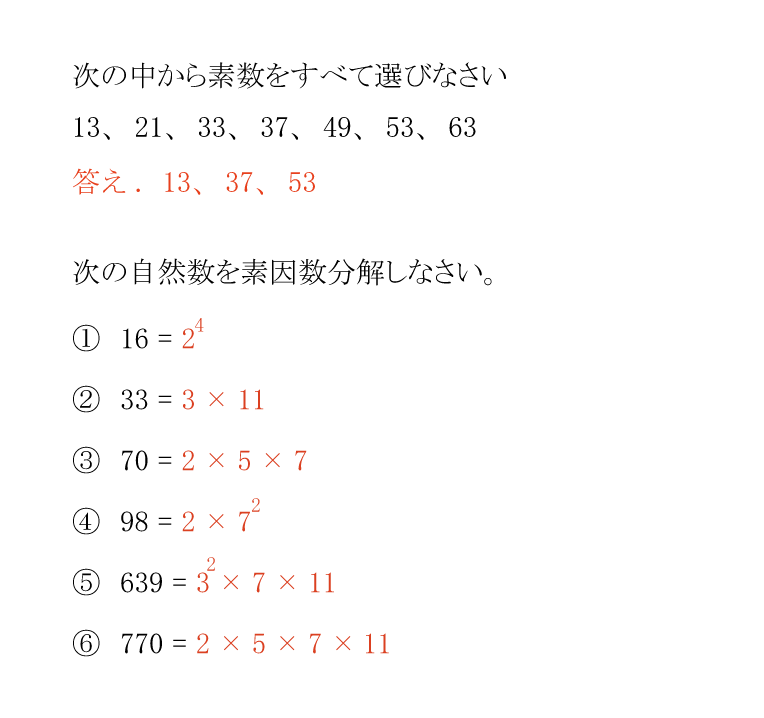
今回は「素数と素因数分解」を勉強したね。
正負の数とはあまり関係がなかったけど、数の基本を学ぶ上でとっても大事なところだからね。
中3で勉強する「平方根」でも、素因数分解が出てくるから、ちゃんと覚えておくんだよ!
正負の数の分野はここまで。
次からは新しい分野の「文字の式」を勉強するよ。
アルファベットの文字を使って、式を作ったり、計算をカンタンにしたりするやつだよ。
次回の勉強部屋はこちら!
>>文字の式
